Research report - Buy signal from rising trend
23 November 2012
Originally published in Norwegian on 3 December 2009.
Investtech was established in 1997 and works with research within behavioural finance. The company has developed an analysis system that identifies trends, support and resistance, formations and volume patterns in stock prices, and generates buy and sell signals on this basis. Investtech uses advanced mathematical algorithms and statistical methods in computer programmes and online subscription services. Mr Asbjørn Taugbøl is a researcher and senior analyst with Investtech. Mr Geir Linløkken is the Founder and Head of Research & Development.
Keywords:
Finance, technical analysis, trend, buy signals, price prediction.
Abstract:
Trends are some of the most important elements in the theory of technical analysis, and are widely used by investors as basis for investment decisions. A rising trend is the result of investors’ on-going optimism. The theory says that stocks in a rising trend will continue to move within the trend. To what extent is this true and can it be used to get excess return? This report is based on research work which indicates that stocks which enter a rising trend as identified by Investtech’s automatic analysis systems give significantly better return than benchmark in the time period following the signal.
Trends
Trends are one of the most important elements of technical analysis. They are visual and intuitive and describe in which direction a stock is moving. A rising trend indicates lasting and increasing optimism among investors, often as a result of a great deal of positive news about the stock.
The trend gives the rate of increase for the stock price, and extrapolating trend lines gives the price target for the stock. There are gradual transitions between rising trends, horizontal trends and falling trends.
The literature on the subject states that "The trend is your friend", meaning that stocks in rising trends will continue to rise within the trend channel. With this starting point, it is important to identify and buy stocks as early as possible after a rising trend is established.
Identifying a trend requires studying the price movements. Stock prices rarely move in a straight line. Instead they move in a series of tops and bottoms. Drawing a straight line through two or more rising bottoms produces the support line in a rising trend. See figure 1. Continue to draw a line parallel to the support line thought the rising tops. This line is called the trend’s resistance line. Support and resistance lines combined make up the trend, see figure 2.
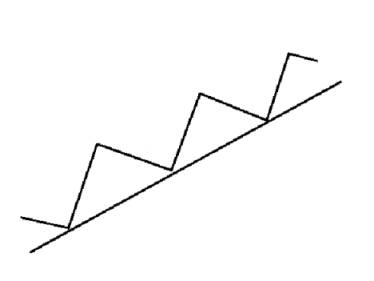
Figure 1.
Support line in a rising trend.
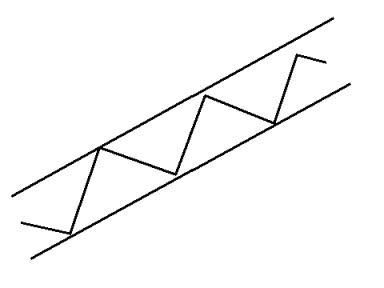
Figure 2.
Rising trend with support line and resistance line.
Similarly, a falling trend is produced when a straight line can be drawn through two or more falling tops and a parallel line through falling bottoms.
Many investors identify trends by studying charts and drawing trend lines by hand. This method has many weaknesses, the most important of which is that it is subjective. You see the trends you want to see and which perhaps fit your own subconscious preferences. It is also a very time consuming method. Investtech has developed automatic algorithms for identification of trends. Every day these algorithms identify the “best” trend in the chart, on criteria such as distance between the trend’s support and resistance lines and the number of data points near these lines. Roughly 80,000 various trend alternatives are assessed each day for a medium term Investtech chart with 18 months of historical data. These are given a score and the best trend is selected.
Figures 3 and 4 show a rising and falling trend, respectively.
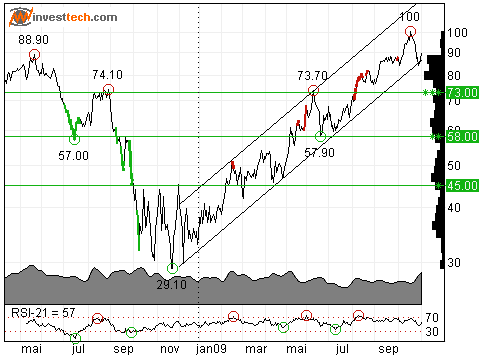
Figure 3. Example of Investtech chart with rising trend.
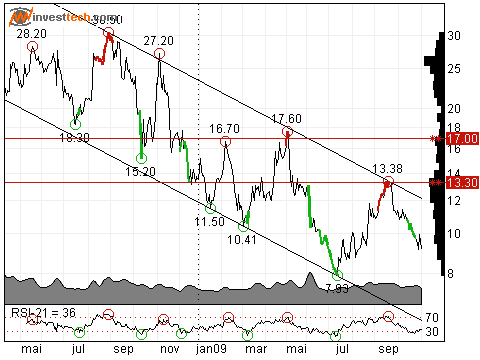
Figure 4. Example of Investtech chart with falling trend.
The Research Project
This report is based on a research project on trends and return as a function of the trend situation. The aim was to find out if there are situations that can be used in practice to achieve excess return by investing in listed stocks. For instance, does buying stocks in rising trends give better return than benchmark? The research work is based on analysis of buy and sell signals from trends identified in Investtech’s charts. We have investigated return as a function of time since the signal from the rising trend and compared to benchmark. There are no requirements for how long the stock must remain in the trend.
The Data Set
We have used historical prices for the companies listed on the Oslo Stock Exchange in the period 1 January 1996 to 30 September 2009 and the companies listed on the Swedish Stock Exchange OMX Stockholm in the period 1 April 2003 to 30 September 2009. Only analyses for companies where average daily turnover in the past 22 days was over NOK 0.5m are included.
Stock prices are adjusted for splits, subscription rights, mergers, dividend payments and other corporate actions, to ensure that the price development mirrors the actual value of the companies. All companies that have been listed on the exchange in the time period studied are included, also companies than are no longer listed today.
Benchmark for the analysis of companies listed on the Oslo Stock Exchange is the OSEBX. For the Swedish Stock Exchange, benchmark is the OMX Stockholm PI.
For recent signals that lack a complete price history for 250 days following the signal date, future price change is estimated to be zero. This has been done instead of removing them from the statistics. For instance, a trade made 100 days ago will have its actual price development in the first 100 days of the statistics, whereas the price after this is estimated to remain unchanged. This is done in order to get the best possible picture of the actual price development.
Buy signals are triggered on the first day the stock enters a rising trend. A rising trend is defined by a rate of increase of more than 10 degrees. Before a buy signal is triggered, the stock may have been above or below a rising trend, in or outside of a falling trend, or not been in any trend. The trends are automatically identified and plotted in Investtech’s medium long charts, and it is a requirement that it has been more than five days since last time the stock was in a rising trend. Sell signals are triggered on the first day the stock enters a falling tend on medium long term and it has been at least five days since last time the stock was in a falling trend. A falling trend is identified by a rate of increase of less than -10 degrees.
The Norwegian data set is comprised of 3747 buy signals and 2792 sell signals. The Swedish data set is 4021 buy signals and 2608 sell signals. See the Appendix for data set details.
Results
Stocks with buy and sell signals from trends on the Oslo Stock Exchange in the period 1996 to 2009 have yielded an average return as shown in figure 5.
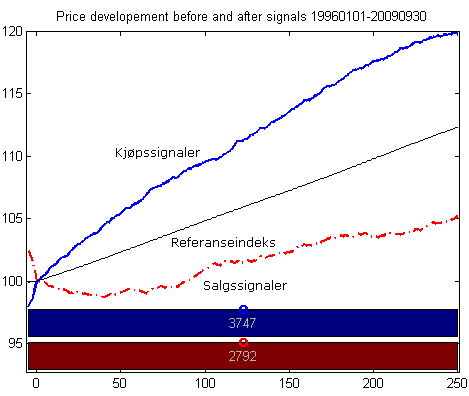
Figure 5: The chart shows average price development five days before signal and one year after signal for Norwegian stocks in the period 1996-2009.The blue curve is buy signals, when the stock enters a rising trend. The red curve is sell signals, when the stock enters a falling trend. The black line shows average price development for benchmark in a sliding time period of one year for the given date interval.
The blue curve, i.e. buy signals, is above the black line after the signal date, and the red curve, i.e. sell signals, is below the black line after the signal date. This shows that buy signals, i.e. buying a stock when it enters a rising trend, on average have a positive price development vis a vis average benchmark development. Similarly sell signals, i.e. buying stocks after they enter a falling trend, on average have a negative price development vis a vis benchmark development. In Norway (figure 5) stocks after buy signal have an average return after one month of 2.7 % and after 12 months of 20.0 %, vis a vis the stock exchange average of 1.0 % and 12.3 % respectively. Sell signals, i.e. stocks that enter a falling trend, on average fall by 1.1 % the first month. After one year, stocks with sell signals from falling trends have on average risen by 5.2 %, i.e. by 7.2 percentage points less than benchmark.
The calculation of average development for stocks with buy signals from trends is made based on a whole 3747 cases. The uncertainty of the estimate, measured by standard deviation, is thus fairly low. In addition, the average return for buy signals 22-250 days after the signal date is between 6.7 and 8.1. standard deviations above benchmark development. Figures this high are considered clearly significant.
Stocks with buy and sell signals from trends on the OMX Stockholm in the period 2003 to 2009 have yielded an average return as shown in figure 6.
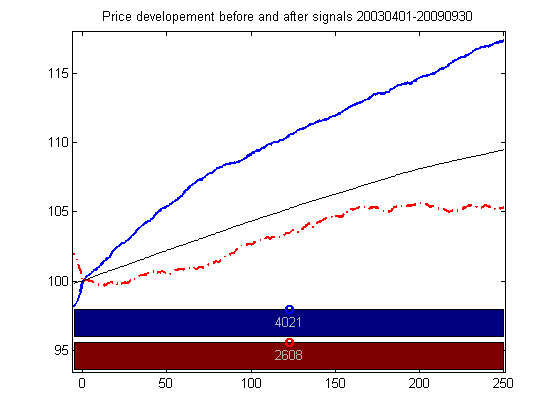
Figure 6: The chart shows average price development five days before signal and one year after signal for Swedish stocks in the period 2003-2009. The blue curve is buy signals, the red curve is sell signals and the black line is average price development for benchmark in a sliding time period of one year for the given date interval.
The same tendency is seen in Sweden (figure 6) as in Norway. The blue curve, buy signals, is above the black line, benchmark, after the buy signal is triggered, and the red curve, sell signals, is below the black line after the sell signal is triggered. After one month buy signals give a return of 2.5 %, and 17.5 % after one year, vis a vis the benchmark average of 1.5 % and 9.0 % respectively. Sell signals on average give a negative return of 0.2 % after one month and a return of 5.3 % after one year.
The number of buy signals is 4019, i.e. a few more than in Norway, and as such the uncertainty of the estimates of average development is quite low. Average return for buy signals 22-250 days after signal is between 5.2 and 9.9 standard deviations above benchmark return. Figures this high are considered clearly significant.
In Norway and Sweden both, stocks entering a rising trend yield better return than benchmark, whereas stocks entering a falling trend yield lower return than benchmark. In addition, as figures 5 and 6 both show, the excess return increases the most in the first 3-4 months following the signal.
We also looked at the yearly variations in excess return from stocks that have given buy signals from rising trends. Great variation here would weaken the overall results, but also indicate in which situations this strategy works very well and in which it does not do so well.
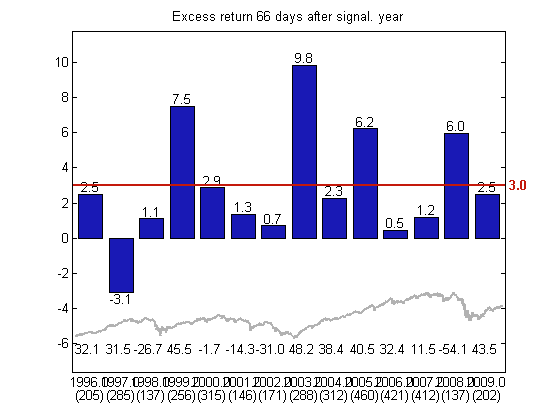
Figure 7: Excess return 66 days after buy signal for Norwegian stocks, split by the year the signal was triggered. The upper half of the figure shows, for Norwegian stocks, excess return 66 days after buy signal from rising trend compared to annual benchmark since 1996. The blue pillars show excess return after 66 days. The red horizontal line shows average excess return after 66 days for all signals. The bottom half of the figure shows benchmark development in the same period, with annual return stated. In parentheses the number of buy signals per year.
In the period 1996 to 2009, benchmark has had both positive and negative annual return. Naturally positive years give more buy signals than negative years, but for a period of 14 years, 13 of them gave positive excess return. There are also no specific years that especially contribute to the overall excess return. A strategy based on buy signals from rising trends thus seems to withstand yearly fluctuations.
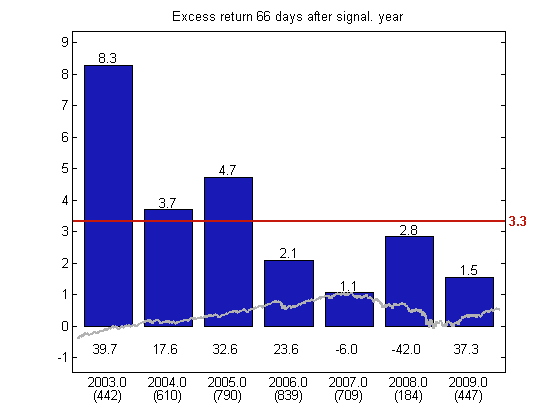
Figure 8: Excess return for Swedish stocks 66 days after buy signal from rising trend as a function of the year the signal was triggered.
All these years have given positive excess return. As in Norway, the exchange has had years with positive and negative return, so the strategy appears able to withstand natural exchange fluctuations here as well.
Conclusion
Stocks with buy signal from rising trends have consistently given good results over time, with significant excess return compared to benchmark.
Based on historical prices for the stocks on the Oslo Stock Exchange from 1996 to 2009 and the OMX Stockholm from 2003 to 2009, stocks that have entered rising trends have outperformed benchmark the following year. Buy signals give a fairly regular increase in excess return for the whole period following the signal date, but with a somewhat higher rate of increase the first 3-4 months. Similarly sell signals give negative return and lower excess return.
The trends were identified by Investtech’s completely automatic systems over a quite long period of time. This gives a great number of signals, so the data are considered good and the results statistically significant. The research shows fair excess return over time, with excess return in 13 out of 14 years in Norway and 7 out of 7 in Sweden. The results are not sensitive to whether the overall stock exchange in the period rises or falls.
Most well-functioning stock exchanges are influenced by the same mechanisms as the Norwegian and Swedish stock exchanges. Central psychological factors such as greed and fear are assumed to be the same for investors worldwide. As such there is reason to believe that the overall conclusions of this report will also be valid in other markets.
Literature
- Geir Linløkken og Steffen Frölich. Technical Stock Analysis – for reduced risks and increased return. Investtech.com, 2001.
- John J. Murphy. Technical Analysis of the Financial Markets. New York Institute of Finance, 1999.
- Geir Linløkken. Buy signals from rectangle formations. Investtech.com, 2005. (In Norwegian.)
- Geir Linløkken. Today’s case – results in a turbulent market. Investtech.com, 2009. (In Norwegian.)
Apppendix
Overview of all buy and sell signals from rising and falling trends identified in the research project:
Investeringsaanbevelingen worden gedaan door Investtech.com AS ("Investtech"). Investtech garandeert geen volledigheid of juistheid van de analyses. Eventuele fouten in de aanbevelingen, koop- en verkoopsignalen en mogelijke negatieve gevolgen hiervan zijn geheel het risico van de belegger. Investtech neemt geen enkele verantwoordelijkheid voor verlies, direct of indirect, als gevolg van het gebruik van Investtechs analyses. Meer informatie omtrent Investtechs analyses kunt u vinden op disclaimer.
Investeringsaanbevelingen worden gedaan door Investtech.com AS ("Investtech"). Investtech garandeert geen volledigheid of juistheid van de analyses. Eventuele fouten in de aanbevelingen, koop- en verkoopsignalen en mogelijke negatieve gevolgen hiervan zijn geheel het risico van de belegger. Investtech neemt geen enkele verantwoordelijkheid voor verlies, direct of indirect, als gevolg van het gebruik van Investtechs analyses. Meer informatie omtrent Investtechs analyses kunt u vinden op disclaimer.


 Oslo Børs
Oslo Børs Stockholmsbörsen
Stockholmsbörsen Københavns Fondsbørs
Københavns Fondsbørs Helsingin pörssi
Helsingin pörssi World Indices
World Indices US Stocks
US Stocks Toronto Stock Exchange
Toronto Stock Exchange London Stock Exchange
London Stock Exchange Euronext Amsterdam
Euronext Amsterdam Euronext Brussel
Euronext Brussel DAX
DAX CAC 40
CAC 40 Mumbai S.E.
Mumbai S.E. Commodities
Commodities Currency
Currency Cryptocurrency
Cryptocurrency Exchange Traded Funds
Exchange Traded Funds Investtech Indices
Investtech Indices
